Compound Interest Explained Clearly: It’s easier than you think!
Ever heard of compound interest when dealing with your bank or mortgage lender? Ever had to use the formula needed to calculate it?
Compound interest may sound like a complicated subject and something only finance and math geeks would use and calculate.
I will not need this so why bother learning what this is. Right?
Wrong!
The compound interest formula is hugely important and useful and we believe it is very important that you understand not only what it is but also how to use it and most importantly how to calculate it.
By the end of this article you will understand fully what compound interest is and that is our promise!
But why do I need to learn this?
Compound interest is used everywhere. Your bank uses it. Every investor in the world is using it. Your mortgage lender is using it. Your credit card company is using it. Employers sometimes add questions about this topic in aptitude tests for new applicants. The list goes on…
In short it is like this: You need to understand the compound interest formula because you will benefit yourself a great deal financially if you do and we all like a bit of extra money in our pocket right?

So what is compound interest?
Compound interest is in short interest on interest.
A more detailed explanation would be that it is the result of reinvesting the interest that you earn from a deposit, rather than cashing it out, meaning that in the next period you will earn interest not only on the deposit amount but also on the interest that you earned in the previous period (i.e. accumulated interest).
Wikipedia explains compound interest like this.
Want another example and explanation? Then check this video out:
Confused? Well there is no need. It is actually very simple. Let me explain it in steps.
Let’s say you have 100 dollars. You have no use for this money right now so you decide to invest this money.
You have a friend who needs money so they tell you that they can pay you 5% interest if they can borrow your 100 dollars for 1 year.
You think this is a good deal as you trust your friend will pay it back and also since you don’t need the money then it is better that someone pays you interest for borrowing it as at the end of the 1 year you will have 105 dollars (100*5%+100).
The calculation above is actually the most common type of interest calculation and is known as simple interest.
Let’s say after year 1 your friend tells you: Thanks for the loan, you really helped me big time. I was wondering if I could keep the money for now and pay you back in another year?
You think why not as you still don’t need the money. So you tell your friend that he can keep the money but as he now owes you 105 dollars that he will have to pay back in 1 years’ time 5% on 105 dollars plus the amount of 100 dollars that he borrowed from you. He agrees.
What happened here in this step is compound interest ladies and gentlemen.
How come you may ask? Well let’s break it into 2 steps and compare them.
If your friend only borrowed 100 dollars for a year and paid you 105 dollars at the year end and then again borrowed another 100 dollars and paid back 105 at the end of year 2 you would have 110 dollars (100 + 5 + 5).
But since you now understand compound interest and your friend didn’t, you actually earned more than 10 dollars simple interest.
You earned:
105*5%+105 = 110.25 dollars.
You earned 0.25 dollars more. This is the compounded interest you just earned.

Your interest of 5 dollars from year 1 just earned you interest at 5% so you made an extra 0.25 dollars.
Whoopee doo…
0.25 dollars is nothing you might think.
Perhaps true but imagine the loan wasn’t 100 dollars but instead it was 1 million dollars.
You would now have made an extra 2 500 dollars ((1 000 000*5%)*5%) just on compound interest.
The bigger the loan amount the bigger the compound interest so as you can see this stuff matters.
That still doesn’t impress me
Well then I have something else that might change your mind and it is time. More specifically the longer the time of the loan the more compound interest can be accumulated.
Let’s look at another example:
Jay wants to invest his inheritance of 100 000 dollars. He manages to find someone who would be happy to pay him 6% annually for 5 years.
So what will Jay have at the end of year 5?
Year 1: 100 000*5% = 5 000
Year 2: 105 000*5% = 5250
Year 3: 110 250*5% = 5512.5
Year 4: 115 762.5*5% = 5788.125
Year 5: 121 550.625*5% = 6077.53
Total compound interest:
5000+5250+5512.5+5788.125+6077.53 = 27 628.155 dollars
What would total simple interest have been? It would just have been 5 000*5 = 25 000 dollars.
So in this case you just made 27 628.155 – 25 000 = 2 628 dollars roughly.
This is the true meaning of “putting your capital to work” as not only is your capital, or principal as it is also called, earning you interest but also your interest is earning you interest.
Ok I get it, I need this. But how do I calculate this using a formula?
Here we get to the interesting part and let’s go straight to the point. You will need these formulas below:
Annually compounded interest formula:
![]()
Half-yearly compounded interest formula:
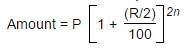
Quarterly compounded interest formula:
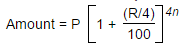
Compounded interest formula with varying interest rates:
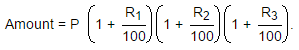
Here, Principal sum = P, Interest = R% per annum, Time = n years
You could also calculate monthly and weekly compounded interest or even daily, there is no limit really, but we will only look at these above.
Let’s look at another example:
Lisa borrows 1000 from her bank for 3 years with an annually compounded interest of 3%. What is her total compounded sum and interest only at the end of year 3?
This means:
1000(1 + 3%/100)^3
Total compounded sum = 1092.727
Total interest: 92.727
Easy right?
Well like we told you this actually is easy but tremendously useful at the same time.
Want to know learn another secret about compounded interest?
The more often you compound, the more you earn.
There it is. The secret truth about why compounded interest is so powerful.
Not only are you earning, or paying out, interest on interest, but the more often the interest is compounded, the more you are paying.
This might not make sense to you now but I will give you another example of compounding the interest quarterly next with the same numbers as above and you can compare then compounding annually to compounding quarterly.
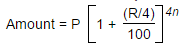
The quarterly compounding formula is above.
Remember, Lisa wanted to borrow 1000 for 3 years at 3% but now the interest is compounded quarterly!
This means:
1000(1 + (3%/4)/100)^4*3
Total compounded sum = 1093.80
Total interest: 93.80
Wait a minute! Lisa is paying more!
Yes she is and that is the secret of compounding more frequently.
Again the difference might not seem a lot but imagine you had a mortgage of 300 000 dollars which was compounded quarterly and you had it for 20 years. Trust me, it adds up in a big way!
Recap
You learnt from this post that compound interest is powerful and can either earn you more money or cost you more money than simple interest.
Interest earnt on interest is always extra money.
You also learnt that the frequency of how often the interest is compounded matters and in fact the more frequently this is done the bigger the amount of compounded interest.
And last you now have all the compound interest formulas needed to do all the calculations yourself.
Hope this was helpful and please add your comments and suggestions in the discussion box below and remember to like us on social media as well.
Want to practice and become fluent in compound interest calculations? Try these practice compound interest formula test questions.


