Compund Interest Formulas with Questions and Answers

Home > Numerical Tests > Compound Interest Formula > Compound Interest Questions
![]()
Being able to calculate compound interest is not just good when taking aptitude tests but also in normal day to day life.
You will need it for any loan that you take or calculate the interest on. Compound interest is one of the greatest things in finance to understand and master so it is vital that you know these formulas below and practice on the questions here as well. You won't regret it!
For a detailed and easy to understand explanation about compound interest please read our blog article!
Compound interest is actually a very simple concept. Normally you would have two things in a loan or investment, a principal sum and interest.
The principal sum is the amount that you borrowed or invested and the interest is the interest that you would pay or receive in order to borrow/lend the principal sum.
What compunded interest then means is that you pay or receive interest on the interest i.e. it is compounding. Let's look at an example to make it easier.
You invest 100 (principal sum) and the return you expect is 10% (interest rate).
End of year 1 your investment will then have made you 10 as 10% of 100 is 10. So end of year you principal sum plus the return of 10 is then 110.
If you decide that you want to invest again in year 2 and you don't take out the 10% interest you just earned but instead you reinvest it then your investment in year 2 would be 110 and the interest is again 10%.
At the end of year 2 you would now then have made 10% on 110 and not on 100. In other words your return at the end of year 2 is 11 (10% of 110).
Now compare the two: 10 and 11.
What has happened here is the effect of compounded interest!
You have compounded the interest from year 1 which was 10 to 11 in year two.
Not only have you now increased your principal amount from 100 to 121 (100+10+11) but have now made the interest received also work for you as they say in finance, i.e. you have reinvested your returns and not taken them out.
It may seem like a small amount to receive 1 extra unit but next year it will increase and the next and the next like this:
100*10%=110
110*10%=121
121*10%=133.1
133.1*10%=146.14 etc...
If you would have invested only the principal amount each year you would only have 140 and not 146.41.
Imagine now if the investment is not 100 but instead 1 000 000! Compound interest is great when investing. But also remember when you are borrowing money, then compound interest goes aginst you as you will start paying interest on interest.
Please find our compound interest formulas below:
Annually compounded interest formula:
![]()
Half-yearly compounded interest formula:
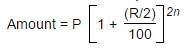
Quarterly compounded interest formula:
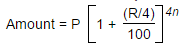
Compounded interest formula with varying interest rates:
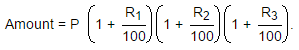
Here, Principal sum = P, Interest = R% per annum, Time = n years
Test your knowledge below:
You have an investment proposition in front of you where you would invest 150 dollars in a project and after 2 years you can sell the investment. You would earn 5% paid annually. How much would you have at the end of year 2?
Answer & Explanation:
Answer: Option B
Explanation: Use the annual formula above to come to the answer.
You have an investment proposition in front of you where you would invest 1000 dollars in a project and after 4 years you can sell the investment. You would earn 4% paid annually. How much would you have at the end of year 4?
Answer & Explanation:
Answer: Option A
Explanation: Use the annual formula above to come to the answer.
You have an investment proposition in front of you where you would invest 100 dollars in a project and after 2 years you can sell the investment. You would earn 5% paid annually OR you can receive the interest quarterly. Which one should you go for?
Answer & Explanation:
Answer: Option C
Explanation: It is better to receive the interest quarterly as then you are receiving money more frequently and can reinvest that right away after quarter 1 instead of waiting the full year and then reinvest.
You have an loan proposition in front of you where you would borrow 100 000 dollars for a boat and after 2 years you can pay back the loan and not earlier. You would pay 3% paid annually. How much would you owe at the end of year 2?
Answer & Explanation:
Answer: Option D
Explanation: Use the annual formula above again.
If in the question above the interest was calculated half-yearly, what would the final loan amount be with interest?
Answer & Explanation:
Answer: Option C
Explanation: Use the half-yearly formula above. Just because the interest on the loan is now compounded half-yearly you are ending up paying 106136-106090=46 more than when just annually compounded!
Page 1 | Page 2 | Page 3 | Page 4 |
![]()


