Numerical Ability Questions and Answers

Home > Numerical Tests > Numerical Ability > Numerical Ability Questions
![]()
A boat can travel with a speed of 13 km/hr in still water. If the speed of the stream is 4 km/hr, find the time taken by the boat to go 68 km downstream.
Answer & Explanation:
Answer: Option C
Explanation: Speed downstream = (13 + 4) km/hr = 17 km/hr.
Time taken to travel 68 km downstream = 68/17 hrs = 4 hrs.
A man's speed with the current is 15 km/hr and the speed of the current is 2.5 km/hr. The man's speed against the current is:
Answer & Explanation:
Answer: Option C
Explanation: Man's rate in still water = (15 - 2.5) km/hr = 12.5 km/hr.
Man's rate against the current = (12.5 - 2.5) km/hr = 10 km/hr.
A boat running upstream takes 8 hours 48 minutes to cover a certain distance, while it takes 4 hours to cover the same distance running downstream. What is the ratio between the speed of the boat and speed of the water current respectively?
Answer & Explanation:
Answer: Option C
Explanation: Let the man's rate upstream be x kmph and that downstream be y kmph.
Then, distance covered upstream in 8 hrs 48 min = Distance covered downstream in 4 hrs.
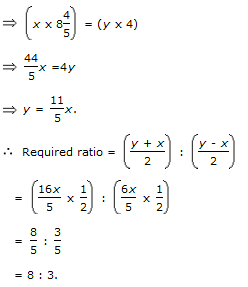
A motorboat, whose speed in 15 km/hr in still water goes 30 km downstream and comes back in a total of 4 hours 30 minutes. The speed of the stream (in km/hr) is:
Answer & Explanation:
Answer: Option B
Explanation: Let the speed of the stream be x km/hr. Then,
Speed downstream = (15 + x) km/hr,
Speed upstream = (15 - x) km/hr.
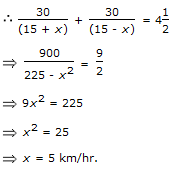
In one hour, a boat goes 11 km/hr along the stream and 5 km/hr against the stream. The speed of the boat in still water (in km/hr) is:
Answer & Explanation:
Answer: Option C
Explanation: Speed in still water = 1/2x(11 + 5) kmph = 8 kmph.


