Compounded Interest

Home > Numerical Tests > Compounded Interest > Compounded Interest Questions
![]()
Please find our compounded interest questions and formulas below. To understand compound interest fully please read our blog article on it!
Annually compounded interest formula:
![]()
Half-yearly compounded interest formula:
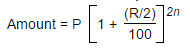
Quarterly compounded interest formula:
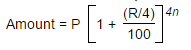
Compounded interest formula with varying interest rates:
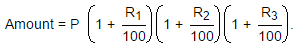
Here, Principal sum = P, Interest = R% per annum, Time = n years
You invest Yen 1000 in a 100 year bond but only receive 1% annually. How much would you have received interest in total after 100 years?
Answer & Explanation:
Answer: Option A
Explanation: Use the annual formula above to come to the answer. 1.01^100*10000-10000=1704.81=1705
Igor the loanshark is harrassing you because you haven't paid back that loan of yours. He is not very clever so he says "pay me 10% on the 1000 that you borrowed". You have had the loan for 1 year so you ask if it is calculated annually? He thinks your are stupid and says "of course it is" and kicks you out. If he would have said quarterly, then how much more in interest would you have had to pay?
Answer & Explanation:
Answer: Option B
Explanation: Use the quarterly yearly formula above to come to the answer. 10/4=2.5% 1.025^4*1000=1103.81-1000=103.81 With 10% annual you would have paid 1000*0.1=100
You stumble upon a great investment proposal where you are offered 25% annually for ever. How long would it take to increase 1000 to 10000 i.e. 10 times in years?
Answer & Explanation:
Answer: Option C
Explanation: 1.25^9=9.313 and 1.25^10=11.641 i.e. it would take just over 10 years to do it. 1.0125^40*25000-25000=16090
A rich family has been investors for decades. It all started when Alfred invested all his money in a chocolate factory. He invested 1 000 000 euros 150 years ago earning on average 10% per annum. How much would his investment be worth today 150 years later if compounded annually?
Answer & Explanation:
Answer: Option D
Explanation: Use the annual formula above again here. So now we have 1 000 000*((1+(10%)))^(150)=4 448 423.
If you can choose how frequently the interest rate on a loan is compounded that you have to pay back to someone else. In order to pay the least amount of interest would you want it rather to:
Answer & Explanation:
Answer: Option B
Explanation: By compounding annually you would pay less interest than monthly compounding for example so B is the right answer.
Page 1 | Page 2 | Page 3 | Page 4 |
![]()


