Compund Interest Questions and Answers

Home > Numerical Tests > Compound Interest > Compound Interest Questions
![]()
Please find our compound interest formulas below. To understand compound interest fully please read our blog article on it!
Annually compounded interest formula:
![]()
Half-yearly compounded interest formula:
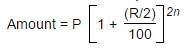
Quarterly compounded interest formula:
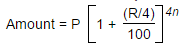
Compounded interest formula with varying interest rates:
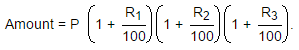
Here, Principal sum = P, Interest = R% per annum, Time = n years
You have an investment proposition in front of you where you would invest 25000 dollars in a project and after 10 years you can sell the investment. You would earn 5% paid annually. How much would you have at the end of year 10?
Answer & Explanation:
Answer: Option C
Explanation: Use the annual formula above to come to the answer. 1.05^10*25000
In the above investment you are given the option to receive the interest compounded half-yearly as well. How much would you now have after year 10?
Answer & Explanation:
Answer: Option D
Explanation: Use the half yearly formula above to come to the answer. 5/2=2.5% 1.025^20*25000=40965
What if in the investment above you could receive the interest quarterly? How much interest would you have accumulated after 10 years?
Answer & Explanation:
Answer: Option A
Explanation: 5/4=1.25% 1.0125^40*25000-25000=16090
The investment provider is going all out! He is offering you monthly compounded interest payments. What would your principal plus interest be at the end of year 10 now?
Answer & Explanation:
Answer: Option B
Explanation: Use the annual formula above again but as we have monthly interest we divide the annual interest rate by 12 months and we also multiply n=10 years by 12 months so we have 120. So now we have 25000*((1+(5%/12)))^(10*12)=41175.
How much more interest + principal in total percentage wise would you receive when you compare the annual to the monthly compounded?
Answer & Explanation:
Answer: Option C
Explanation: Monthly was 41175 and annual was 40722 with a difference of 453. 453/40722=1.11% more just by choosing to receive the interest more frequently.
Page 1 | Page 2 | Page 3 | Page 4 |
![]()


